1. 개요
동적 계획법 ( Dynamic Programming, 줄여서 DP ) 은 프로그래밍 대회에서 출제되지 않으면 이상할 정도로 높은 출제빈도를 보이고 있을 만큼 중요한 알고리즘 설계 기법입니다. 동적 계획법은 주어진 문제를 여러 개의 하위문제들로 나누어 먼저 처리한 후 그 답들을 이용해 문제를 처리하는 방법을 뜻합니다. 하위문제들을 수행할 시에는 같은 문제를 여러 번 처리하는 경우가 발생하는데 이 때, 한번 수행한 문제들의 답을 저장해 놓으면 그 다음부터는 답을 바로 알아낼 수 있어 속도가 비약적으로 빨라지게 할 수 있습니다.
2. DP 기본 예제 – 피보나치 수열
피보나치 수열은 F[0] = 0, F[1] = 1, F[i] = F[i-1] + F[i-2] ( i > 1 ) 을 만족하는 수열인데 n이 주어졌을 때 DP를 이용하여 F[n]을 구해보도록 하겠습니다. 우선 F[i] = F[i-1] + F[i-2]라는 점화식이 성립하므로 F[n] 을 구하기 위해선 F[n-1], F[n-2]라는 하위문제의 답을 먼저 구해야 합니다. 이를 재귀함수로 해결하면 아래의 코드 1-1과 같이 됩니다.

위 함수를 이용하여 F[4]를 구하면 아래와 같이 함수들이 호출됩니다.
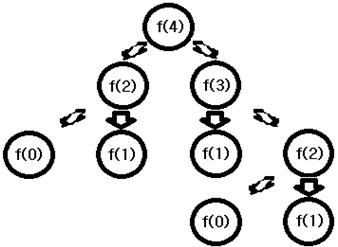
위의 그림을 보면 함수가 정답을 알아내긴 하지만 f(0), f(1), f(2) 등 여러 번 호출되더라도 같은 값을 return하는 함수가 호출될 때마다 새로 값을 구하는데 이는 시간복잡도상 굉장한 낭비입니다. 이를 개선하기 위해선 return하는 값을 따로 저장하여 다시 호출되었을 때는 저장한 값을 바로 return하면 되는데 이러한 방법을 ‘메모이제이션’이라고 합니다.

이 코드로 F[4]를 구하면 아래와 같이 함수가 호출됩니다.

코드 1-1 과 달리 처음의 fibonacci(2) 수행시의 결과값을 저장했기 때문에 다음에는 f(0), f(1) 을 호출할 필요가 없어집니다. F[4]는 숫자가 작아 큰 차이가 나진 않지만 n이 커질수록 시간의 차이가 기하급수적으로 늘어나는 것은 쉽게 확인할 수 있습니다.
3. DP로 문제에 접근하기
DP로 주어진 문제를 해결하고자 할 때 필요한 것은 1. DP 문제를 정의하는 것, 2. 각 문제의 하위문제를 찾는 것, 3. 하위문제들로 답을 구하는 방법을 찾는 것이 있습니다. 피보나치 예제에서는 하위문제를 F[n-1], F[n-2]로 바로 알아낼 수 있지만 문제가 어려워 질수록 힘들어지게 됩니다. 다음 예제를 통해 DP문제를 단계적으로 해결해 보도록 합시다.
예제 3-1 : 삼각그래프 ( http://www.acmicpc.net/problem/4883 )
위의 문제를 DP문제로 접근하기 위해선 일단 DP문제를 정의해야 합니다. 가장 아래쪽 ‘정점’으로 가는 ‘최소 비용’을 구해야 하므로 자연스럽게 다음과 같이 문제를 정의하게 됩니다.
DP( i, j ) = i행의 j번째 ‘정점’까지 가는데 필요한 ‘최소 비용’.
이제 하위 문제를 정의해야 하는데 i행의 j번째 정점으로 갈 수 있는 정점은 i-1행의 0번째, i-1행의 1번째, i-1행의 2번째 정점만 있으므로 DP( i, j ) 를 구하기 위한 하위 문제는 DP( i-1, 0 ), DP( i-1, 1), DP( i-1, 2)가 될 것입니다.
마지막으로 DP( i, j ) 와 하위문제들 사이의 관계를 알아내면 되는데 우리가 구하고자 하는 것은 최소 비용이므로 다음과 같은 관계가 됩니다.
DP( i, j ) = MIN( DP( i-1, 0 ), DP( i-1, 1), DP( i-1, 2) ) + A[i][j] ( A[i][j] = i행 j번째 정점의 비용 )
이제 이를 구현한 후 정답 = MIN( DP( n-1, 0 ), DP( n-1, 1), DP( n-1, 2) ) 이 됨은 자명합니다.
이처럼 DP로 문제를 접근할 때는 DP문제와 하위문제를 잘 설정해야 해결할 수 있는데, 이 때, 다음 2가지에 유의하는 것이 좋습니다.
1) 문제들을 정점으로, 상위문제 → 하위문제를 간선으로 그래프를 그렸을 때 사이클이 없는 방향성 그래프 즉, DAG( Directed Acyclic Graph ) 가 되도록 정의해야 합니다.
만일 (1)의 조건에 어긋나는 상황, 아래 그림과 같은 상황이 나온다면 무한루프에 빠지는 등 DP로 해결이 불가능하게 됩니다.

위의 조건으로 인하여 만일 문제의 input이 사이클이 존재하는 그래프로 주어진다면 DP의 가능성이 낮아지게 됩니다. ( 변형하여 응용하는 등의 수도 있어 가능성이 없진 않습니다. ) 반대로 만일 input이 tree나 DAG의 형식으로 주어진다면 DP의 가능성을 의심해 보아야 하며 tree DP의 경우 대회에서 종종 출제되고 있습니다.
2) 각 문제를 기준으로 그 전의 계산과정( 하위 문제들 )과 후의 계산과정( 상위 문제들 )이 저장한 정보를 제외하면 서로 독립적으로 분리되어야 합니다.
3-1 예제, 삼각그래프의 DP 계산과정에서 DP( i, j ) 를 기준으로 생각해 보면 DP( i, j ) 의 상위 문제들의 입장에서 i행의 j번째 정점까지 왔을 때의 최소 비용만 알고 있으면 이 최소 비용이 어떠한 계산 과정으로 만들어진 것인지에 대한 정보는 더 이상 필요하지 않습니다.
즉, DP( i, j )가 i-1번째 행 중 몇 번째 열에서 MIN값을 찾았는지 등의 정보가 필요하지 않은 것입니다.
만일 이러지 않고, 0 ~ i-1 번째 행에서 어떠한 경로를 통해 최소비용이 계산되었는지를 알아야 한다면 시간복잡도가 O(3^n) 이상으로 치솟을 수 있으므로 만일 이 것과 비슷한 상황을 만나게 된다면 최대한 독립적으로 계산될 수 있게 DP를 정의하도록 노력해야 합니다. - 연습문제 5번 참조
4. DP 구현하기
DP를 구현하는 방식에는 크게 2가지 방식, 반복적 동적 계획법과 재귀적 동적 계획법이 있습니다. 반복적 동적 계획법은 재귀호출이 아닌 반복문을 통해 구현하는 것이고 재귀적 동적 계획법은 메모이제이션을 통해 구현하는 것입니다.


이 두 가지 방법은 서로 장단점을 가지고 있는데 DP에 대한 감각과 이해도의 향상을 위해서는 두 가지 방법 모두에 익숙해 지는 것이 좋습니다. 특히, 반복적 동적 계획법에 익숙해져 그 것만 사용하는 경우가 있는데 재귀적 동적 계획법의 경우 DP의 정의대로 구현되는 만큼 더 직관적이어서 구현하기 어려운 문제의 경우에 더 편하게 구현할 수 있는 경우가 많이 발생하니 재귀적 동적 계획법도 사용할 줄 아는 것이 좋습니다.
5. 연습문제
(0) https://www.acmicpc.net/problem/2579 ☆
(1) https://www.acmicpc.net/problem/5060 ★
(2) https://www.acmicpc.net/problem/2533 ★☆
(3) http://codeforces.com/contest/235/problem/B ★★
(4) http://codeforces.com/contest/464/problem/C ★★☆
6. 연습문제 해설
(0) 계단 오르기
일단 마지막 계단까지 올라가는 최댓값을 구해야 하고 계단은 한번에 1개 혹은 2개를 올라갈 수 있으니 아래와 같이 설정해 볼 수 있습니다.
DP( i ) = i번째 계단까지 올라가는 최댓값
하위문제 : DP( i-1 ), DP( i-2 )
이 때, 아래에 있는 계단으로 갈 수가 없으니 3 - (1)의 조건, 사이클이 생길 일에 대해선 걱정할 것이 없습니다. 하지만 ‘연속된 세 개의 계단을 모두 밟아서는 안 된다. ’는 조건이 있는데 이 때문에 DP( i-1 ), DP( i-2 )의 정보만 가지고는 처리를 할 수 없어 ( 3 - (2) 조건에 어긋남 ) DP 설정에 정보를 추가하게 됩니다.
DP( i, j ) = 마지막 점프가 j개를 올라가는 점프이며 i번째 계단까지 올라가는 최댓값
하위문제 : DP( i-1, 2 ), DP( i-2, 1 ), DP( i-2, 2 )
( DP( i-1, 1 ) 의 상태에서 i번째 계단으로 가면 조건에 위배되기 때문에 제외 )
이렇게 설정을 추가하면 하위문제만 가지고 답을 구할 수 있게 되어 해결할 수 있습니다. ( 초기의 설정으로도 하위문제의 갯수를 늘리면 해결이 가능합니다. )
DP( i, 1 ) = DP( i-1, 2 ) + 계단 i의 점수
DP( i, 2 ) = max( DP( i-2, 1 ), DP( i-2, 2 ) ) + 계단 i의 점수


(1) 무글 맵스
이 문제의 조건을 관찰하기 위해 간단하게 어떤 저장한 위치 i가 있다고 해봅시다.
그러면 0 ~ i번지의 오차와 i ~ n-1 번지의 오차의 연결 고리는 ‘저장한 집이 몇 개인가’ 가 유일하게 됩니다. DP로 해결하기 위해선 상위문제들과 하위문제들을 최대한 독립적으로 해주어야 합니다.
그러므로 0 ~ i번지 중 저장한 집의 개수가 j개라고 하면 i ~ n-1번지중 저장한 집의 개수는 c-j+1개가 되며 이제 두 문제 사이의 연결고리는 없고 서로 독립적으로 계산이 가능하게 되었습니다.
이제 문제에서 주어진 2가지 n, c와 조건을 이용해 다음과 같이 DP문제를 정의해 봅니다.
DP( i, j ) = 0~i 번지의 집중에 j개를 저장했을 때 오차의 합의 최솟값 ( 단, 0 과 i번지는 반드시 저장해야함 )
이제 DP( i, j ) 를 구할 수 있는 하위문제들과 관계식을 찾아야 하는데 일단 i번지 까지 j개의 저장을 하는 모든 경우의 수를 생각해 보아도 j개를 저장하기 위해선 j-1개를 저장한 단계를 반드시 지나야 하니
하위문제를 DP( 0, j-1), DP( 1, j-1), … , DP( i-1, j-1) 로 설정해 볼 수 있고 이들 중 하나도 거치지 않고 DP( i, j ) 상태에 도달하는 것은 불가능합니다.
이제 식을 생각하면 아래와 같이 됩니다.
DP( i, j ) = MIN ( DP( k, j-1) + error[k][i] ), k = 0 ~ i-1 ( error[k][i] = k,i를 저장했을 때 그 사이 번지들의 오차의 합. )
이제, 답은 DP( n-1, c) / n 이 됨은 당연합니다.


(2) 사회망 서비스(SNS)
일단 인풋으로 트리가 주어지고 있으므로 가장 흔하고 쉽게 생각할 수 있는 DP설정을 사용하면
DP( i ) = i 를 root로 하는 subtree 의 최소 얼리 어답터 수, 하위문제 = DP( i 의 자식들 )
위와 같이 설정해 볼 수 있습니다. 이 상태에서 하위문제들로 DP(i) 를 구해 보면 일단, i가 얼리어답터인 경우, 얼리어답터가 아닌 경우 이 두 가지의 경우의 수가 존재 합니다.
우선 i가 얼리어답터인 경우를 보면 자식 노드들에 대한 아무런 제약이 걸리지 않으므로 ‘ DP(i 의 자식들 )의 총합 + 1 ‘ 임을 쉽게 알 수 있습니다.
이제 문제는 i가 얼리어답터가 아닌 경우인데 이 때는 자식 노드가 무조건 얼리어답터이어야 하므로 이를 계산하기 위해
‘DP2( i ) = i가 얼리어답터일 경우, i 를 root로 하는 subtree 의 최소 얼리 어답터 수’
위와 같은 형식의 자식 노드들에 대한 새로운 정보가 필요함을 알 수 있습니다. 이제 이를 포함하기 위한 새로운 DP설정을 해보면
DP( i, j ) = i의 상태가 j인 경우, i 를 root로 하는 subtree 의 최소 얼리 어답터 수, 하위문제 = DP( i 의 자식들, false ) , DP( i 의 자식들, false )
이와 같이 정의 할 수 있습니다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace::std;
int n;
int dp[1000005][2];
bool visited[1000005];
vector<int> child[1000005];
vector<int> edge[1000005];
void getchild(int now){
visited[now] = true;
for(int i=0 ; i<edge[now].size() ; i++){
int next = edge[now][i];
if(!visited[next]){
child[now].push_back(next);
getchild(next);
}
}
}
int getdp(int now,bool chk){
if(dp[now][chk]!=0) return dp[now][chk];
if(child[now].size()==0) return dp[now][chk] = chk;
if(chk){
int ans=0;
for(int i=0 ; i<child[now].size() ; i++){
int next = child[now][i];
ans += min(getdp(next,false), getdp(next,true));
}
return dp[now][chk] = ans + 1;
}
else{
int ans=0;
for(int i=0 ; i<child[now].size() ; i++){
int next = child[now][i];
ans += getdp(next,true);
}
return dp[now][chk] = ans;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
int u,v;
scanf("%d %d",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
getchild(1);
printf("%d",min(getdp(1,false),getdp(1,true)));
}
'Algorithm' 카테고리의 다른 글
| Brute Force (기초 개념) (0) | 2023.01.14 |
|---|---|
| 만나본 DP 문제 풀이 유형 (0) | 2023.01.01 |
| Dynamic Programming (기초 개념) (0) | 2022.12.03 |
| 백준 문제 추천 (0) | 2022.10.30 |
| BFS(Breadth First Search) & DFS(Depth First Search) (0) | 2022.09.24 |